Question

Writing the equation of the line through two given points(-4,-1) (2,-5). y=mx-b form

Answer 1

So we are given two points and we have to use them to construct the equation of a line in slope-intercept form:

`y=mx+b`

Where m is the slope and b is the y-intercept. With two given points we can construct two equations for m and b. For example, if we know that the line passes through two generic points (A,B) and (C,D) we have the following equations that are the result of taking (x,y)=(A,B) and (x,y)=(C,D):

`\begin{gathered} B=A\cdot m+b \\ D=C\cdot m+b \end{gathered}`

The points we have are (-4,-1) and (2,-5). Then we have A=-4, B=-1, C=2 and D=-5 and the two equations for m and b are:

`\begin{gathered} -1=-4m+b \\ -5=2m+b \end{gathered}`

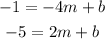
We can take the first equation and add 4m to both sides:

`\begin{gathered} -1+4m=-4m+b+4m \\ b=4m-1 \end{gathered}`

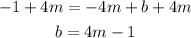
Then we substitute b with this expression in the second equation:

`\begin{gathered} -5=2m+b \\ -5=2m+4m-1 \\ -5=6m-1 \end{gathered}`

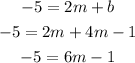
And we add 1 to both sides:

`\begin{gathered} -5+1=6m-1+1 \\ -4=6m \end{gathered}`

And we divide both sides by 6:

`\begin{gathered} -(4)/(6)=(6m)/(6) \\ m=-(4)/(6)=-(2)/(3) \end{gathered}`

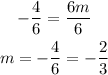
Then we use this value in the expression for b:

`\begin{gathered} b=4m-1=4\cdot(-(2)/(3))-1 \\ b=-(8)/(3)-1 \\ b=-(11)/(3) \end{gathered}`

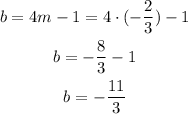
Thent the equation we are looking for and answer to this question is:

`y=-(2)/(3)x-(11)/(3)`