Question

-ln(x) and 1/x go to infinity as X ->0+. Which one goes to infinity faster?

Answer 1

The Solution:

Given the functions below:

`-\ln (x)\text{ and }(1)/(x)`

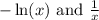
We are required to tell which of them will go to infinity faster as x tends to positive zero.

we shall examine each of the two functions by investigating their slopes under the given conditions.

`\begin{gathered} T\text{he derivative of -}\ln (x)\text{ is }(-1)/(x)\text{ , while that of} \\ (1)/(x)\text{ is }(-1)/(x^2) \end{gathered}`

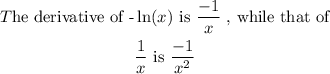
Comparing the absolute values of their slopes at positive smaller values of x, (at x<1 , we get

`\begin{gathered} |(-1)/(x^2)|>|(-1)/(x)| \\ \text{Clearly, the function }(1)/(x)\text{ goes to }\infty\text{ faster as x}\rightarrow0^+ \end{gathered}`

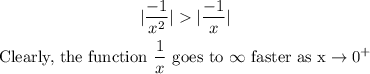
Therefore, the correct answer is 1/x