The magnitude of the electric force between two charged particles is given by Coulomb's Law:
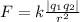
Where q_1 and q_2 are the charges of the particles, r is the distance between the charged particles and k is the Coulomb's Constant:
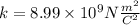
Since the magnitude of both charges is the same, the equation becomes:

The force and the distance between the particles are given, the value of k is known and the charge q is unknown. Isolate q from the equation:
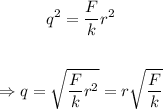
Replace the values of r=24.04*10^-2m, F=87.96N as well as the value of k to find the magnitude of the charges:
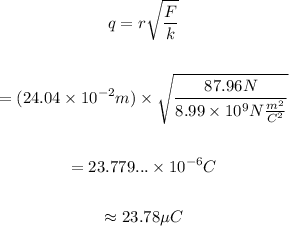
Therefore, the magnitude of the charges in microCoulombs is: 23.78μC.