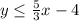Write the inequality shown by the shaded region in the graph of the boundary line negative 5X + 3Y equals -12

Question

asked Aug 15, 2023 98.3k views

1 Answer

Shadmehr Vadoodi · Answer 1 · 2023-08-20T14:08:34+0000

SOLUTION

To do this, we make y the subject of formula in the equation

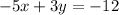
This becomes

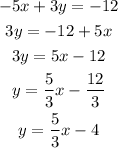
$\begin{gathered} -5x+3y=-12 \\ 3y=-12+5x \\ 3y=5x-12 \\ y=(5)/(3)x-(12)/(3) \\ y=(5)/(3)x-4 \end{gathered}$

Above the line is usually greater than or equal to, while below the line is less than or equal to.

Hence the inequality is

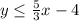
$y\leq(5)/(3)x-4$

Less than or equal to, because it is a solid line and not a broken line

So, the answer becomes

$y\leq(5)/(3)x-4$