Question

(1) 7x+2y=13 (2) 3x+5y=22 Show you work?

Answer 1

x = 0.724

y = 3.966.

Step-by-step explanation:

To solve the system, we need to isolate y in the first equation as follows:

`\begin{gathered} 7x+2y=13 \\ 2y=13-7x \\ y=(13-7x)/(2) \\ y=6.5-3.5x \end{gathered}`

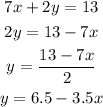
Then, we can replace the value of y by 6.5 - 3.5x on the second equation as follows:

`\begin{gathered} 3x+5y=22 \\ 3x+5(6.5-3.5x)=22 \\ 3x+5(6.5)-5(3.5x)=22 \\ 3x+32.5-17.5x=22 \\ -14.5x+32.5=22 \\ -14.5x=22-32.5 \\ -14.5x=-10.5 \\ x=(-10.5)/(-14.5) \\ x=0.724 \end{gathered}`

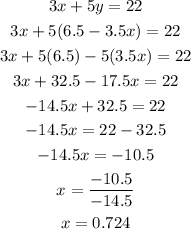
Therefore, the value of y can be calculated as:

`\begin{gathered} y=6.5-3.5x \\ y=6.5-3.5(0.724) \\ y=3.966 \end{gathered}`

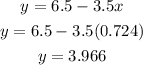
So, the solution of the system is x = 0.724 and y = 3.966.