The ladder reach up to 11.6 ft on the wall.
To solve this, we use trigonometry. We have a hypotenuse of 12ft, and we want to know the lenght of the leg opposite to the angle of 75º. The trigonometric function that relate all 3, is sine:
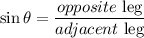
Using the numbers of the problem, and h is the leg we want to find:
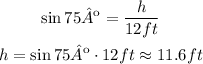
Then the top of the ladder is at 11.6ft from the floor