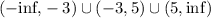Question

Find the domain. Then use the drop down menu to select the correct symbols to indicate your answer in interval notation. If a number is not an integer then round it to the nearest hundredth. To indicate positive infinifty ( \infty ) type the three letters "inf". To indicate negative infinity(-\infty ) type "-inf" with no spaces between characters. f(x)= \frac{2x^3-250}{x^2-2x-15} AnswerAnswer,AnswerAnswerUAnswerAnswer,AnswerAnswerUAnswerAnswer,AnswerAnswer

Answer 1

The domain of a function is all values of x the function can assume.

Since this function has a fraction, and any fraction can't have a denominator equal to 0, we have the following condition:

`\begin{gathered} x^2-2x-15\\e0 \\ x\\e\frac{2\pm\sqrt[]{4+60}}{2} \\ x\\e(2\pm8)/(2) \\ x\\e5,x\\e-3 \end{gathered}`

The variable x can be any real number, except -3 and 5, therefore the domain set is:

`(-\text{inf,}-3)\cup(-3,5)\cup(5,\text{inf)}`