Question

Solve using the Addition Method.5x/6 + y/3 = 4/32x/3 - y/2 = 11/6

Answer 1

`\begin{gathered} (5x)/(6)+(y)/(3)=(4)/(3) \\ (2x)/(3)-(y)/(2)=(11)/(6) \end{gathered}`

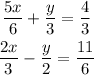
to solve this,

Step 1

the purpose of this method is eliminate a variable by adding the two equations, to do this, you need to be sure that the add will make that variable disappear.

Let's see y

`\begin{gathered} (y)/(3) \\ \text{and} \\ -(y)/(2) \end{gathered}`

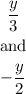
to eliminate y make

`\begin{gathered} multiply\text{ the first equation }by\text{ }(1)/(2) \\ \\ (5x)/(6)+(y)/(3)=(4)/(3)\text{ by }(1)/(2) \\ (1)/(2)\cdot(5x)/(6)+(1)/(2)\cdot(y)/(3)=(1)/(2)\cdot(4)/(3) \\ (5x)/(12)+(y)/(6)=(2)/(3)\text{ equation (3)} \\ \end{gathered}`

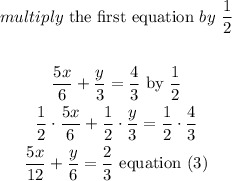
Now, multiply the second equation by 1/3

`\begin{gathered} (2x)/(3)-(y)/(2)=(11)/(6)\text{ by }(1)/(3) \\ (1)/(3)\cdot(2x)/(3)-(1)/(3)\cdot(y)/(2)=(1)/(3)\cdot(11)/(6) \\ (2x)/(9)-(y)/(6)=(11)/(18)\text{ equation (4)} \end{gathered}`

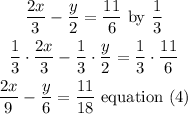
Now, add equations 3 and 4

`\begin{gathered} (5x)/(12)+(y)/(6)=(2)/(3) \\ (2x)/(9)-(y)/(6)=(11)/(18) \\ x((5)/(12)+(2)/(9))=(2)/(3)+(11)/(18) \\ x((23)/(36))=(23)/(18) \\ x=(23\cdot18)/(36\cdot23) \\ x=(414)/(828) \\ \\ x=(1)/(2) \\ \end{gathered}`

Now, with this value of x, find y, replacing in the equation 1 or 2

`\begin{gathered} (2x)/(3)-(y)/(2)=(11)/(6) \\ (2((1)/(2)))/(3)-(y)/(2)=(11)/(6) \\ (1)/(3)-(y)/(2)=(11)/(6) \\ -(y)/(2)=(11)/(6)-(1)/(3) \\ -(y)/(2)=(3)/(2) \\ y=(3\cdot-2)/(2) \\ y=-3 \end{gathered}`

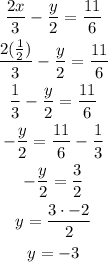
so, the solution is x=0.5 and y =-3

I really hope this helps