EXPLANATION
Let's see the facts:
One month:
Rented movies = 5
Rented video games = 3
Total = $34
Next month:
Rented movies = 2
Rented video games = 12
Total = $73
Let's call x to the rental cost for each movie and y to the rental cost for each game, representing the given data on a system of equations give us the following expressions:
(1) 5x + 3y = 34
(2) 2x + 12y = 73
Now, we need to solve this system of equations:
Isolate x for 5x + 3y = 34:
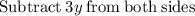
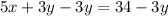
Simplify:
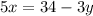
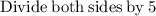
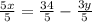
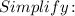
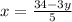
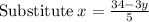
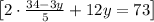
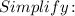
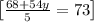
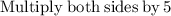
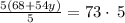
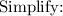
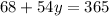
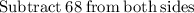
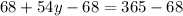
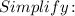
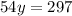
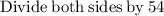
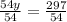
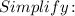
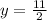
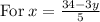
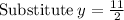
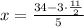
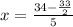
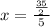
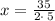
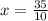
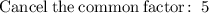
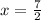
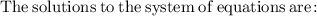
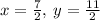
Now, as x=rental cost for each movie and y= rental cost for each video game, we can conclude:
Rental cost for each movie = $3.5
Rental cost for each video game = $5.5