Question

Given the definitions of f(x) and g(x) below, find the value of (fog)(-8).f(x) = x2 – 3x – 12g(x) = -1 – 12

Answer 1

Rewrite the expression using the definition of composite functions.

`(f\circ g)(-8)=f(g(-8))`

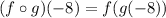
Start from the inner function. To solve for g(-8), substitute -8 into the value of x in g(x).

`(f\circ g)(-8)=f\lbrack-(-8)-12\rbrack`

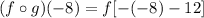
Simplify the expression inside the brackets.

`(f\circ g)(-8)=f(8-12)=f(-4)`

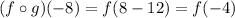
To find f(-4), substitute -4 into the value of x in f(x).

`(f\circ g)(-8)=(-4)^2-3(-4)-12`

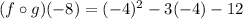
Simplify the expression.

`(f\circ g)(-8)=16+12-12=16`

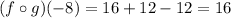
Therefore, the value of the expression is 16.