Question

Solve for x. -5(-x - 4) - 3x – 5 = 13

Answer 1

Given the following equation:

`-5\mleft(-x-4\mright)-3x-5=13​`

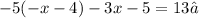
You can solve for the variable "x" by following the steps shown below:

Step 1. Apply the Distributive property by multiplying eact term inside the parentheses by -5:

`\begin{gathered} (-5)(-x)-(-5)(4)-3x-5=13​ \\ 5x+20-3x-5=13 \end{gathered}`

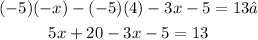
Step 2. Add the like terms on the left side of the equation:

`2x+15=13`

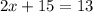
Step 3. Apply the Substraction property of equality by subtracting 15 from both sides of the equation:

`\begin{gathered} 2x+15-(15)=13-(15) \\ 2x=-2 \end{gathered}`

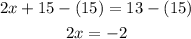
Step 4. Finally, apply the Division property of equality by dividing both sides of the equation by 2:

`\begin{gathered} (2x)/(2)=(-2)/(2) \\ \\ x=-1 \end{gathered}`

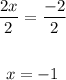
The answer is:

`x=-1`

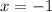
Did you understand?