Question

A backyard garden is shaped like a rectangle with a perimeter of 240ft if the length is twice the width what is the width, the length and the area of the garden

Answer 1

Consider that the area (A) and perimeter (P) of a rectangle with length (L) and width (W) is given by the formulae,

`\begin{gathered} A=L\cdot W \\ P=2\cdot(L+W) \end{gathered}`

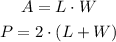
Given that the perimeter of the rectangular garden 240 ft,

`\begin{gathered} P=240 \\ 2\cdot(L+W)=240 \\ L+W=120\ldots\ldots(1) \end{gathered}`

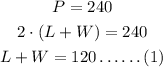
Also, it is given that the length is twice the width,

`L=2W`

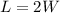
Substitute this in equation (1) and simplify,

`\begin{gathered} 2W+W=120 \\ 3W=120 \\ W=40 \end{gathered}`

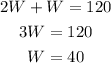
Then the corresponding length will be,

`\begin{gathered} L=2(40) \\ L=80 \end{gathered}`

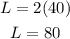
Now that the length and width of the rectangular garden is known, the area can be calculated as,

`\begin{gathered} A=80\cdot40 \\ A=3200 \end{gathered}`

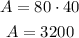
Thus, the length, width, and area of the rectangular garden are 80 feet, 40 feet, and 3200 square feet, respectively.