Answer:
The lines are not perpendicular
Step-by-step explanation:
We are to calculate the slope from the information given to us and to determine if the lines are perpendicular. This is shown below:
Orange line
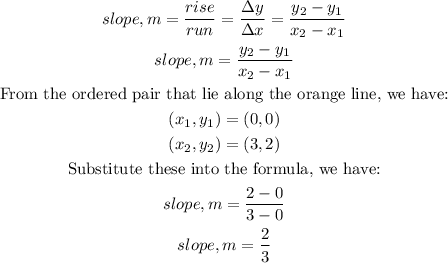
Blue line

For perpendicular lines, the relationship between their slope is that they are negative reciprocals of each other. This is given by the formula:

Therefore, the lines are not perpendicular