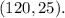To solve the system by substitution, first, we substitute the second equation in the first one and get:
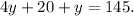
Adding like terms we get:
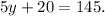
Subtracting 20 from the above equation, we get:
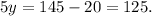
Dividing by 5, we get:
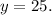
Substituting y=25 in the second equation of the system, we get:
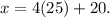
Simplifying the above result, we get:
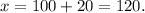
Answer: