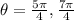Given:
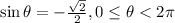
To find:
The two values.
Step-by-step explanation:
It can be written as,
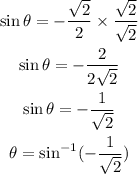
Since the angle lies between 0 and 2π.
Also, the value of the sine function is negative only when the angle lies in the third and fourth quadrant.
So, the angles are,

Final answer:
The values are,