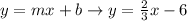So,
To find the equation of the line given, we are going to follow the steps:
1. Identify two points that lie on the line.
As you can see, we could take the points (3 , -4) and (6 , -2).
2. Find the slope between both points. The slope is just the divition of the change of y-units between the points and the change of x-units between the points.
This, is:
3. We could use the main equation of a line:

Where m is the slope and (x,y) is a point that lie on the line.
What we're going to do, is to replace a point (x,y) and the slope that we just found so we can find the value of b and replace these values to find the equation.
So, let's replace (x,y) = (6,-2) and m=2/3:
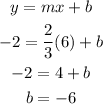
Now, replace m and b in the equation for slope-intercept form: