Question

Use coordinate notation to describe the translation.5 units to the right, 3 units down

Answer 1

We are asked to describe the following translations.

5 units to the right, 3 units down 10​

Let (x, y) is a point on a coordinate plane.

Translation to the right:

5 units to the right, is a horizontal positive (right) translation.

5 units to the right means that add 5 to the x-coordinate.

`(x,y)\rightarrow(x+5,y)`

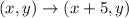
Translation down:

3 units down, is a vertical negative (down) translation

3 units down means that subtract 3 from the y-coordinate.

`(x,y)\rightarrow(x,y-3)`

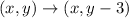
Therefore, the end result after both these translations is

`(x,y)\rightarrow(x+5,y-3)`

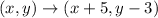
Bonus:

To the right = add to x-coordinate

To the left = subtract from the x-coordinate

Move Up = add to y-coordinate

Move down = subtract from the y-coordinate