Question

An object is thrown upward at a speed of 124 feet per second by a machine from a height of 19 feet off the ground. The height h of the object after t seconds can be found using the equation h = - 16t2 + 124t + 19 When will the height be 59 feet? Select an answer When will the object reach the ground? Select an answer > Next Question

Answer 1

a) For this question we set h=59 and solve for t, in order to do so we use the general formula for second-degree equations:

`\begin{gathered} t=\frac{-124\pm\sqrt[]{124^2-4(-16)(-40)}}{2(-16)} \\ t=(-124\pm113.21)/(-32) \end{gathered}`

The height of the object will be 59 feet at t=7.41 seconds and t=0.34 seconds.

b) When the object reaches the ground, h=0 therefore:

`0=-16t^(2)+124t+19`

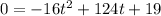
Solving for t we get:

`\begin{gathered} t=\frac{-124\pm\sqrt[]{124^2-4(-16)(19)}}{2(-16)} \\ t=\frac{-124\pm\sqrt[]{16592}}{-32}=(-124\pm128.81)/(-32) \end{gathered}`

Therefore, since t cannot be negative the solution is t=7.9 seconds.