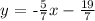Question

Find the equation of the line that contains the point (-1,-2) and is parallel to the line 5x+7y=12. Write the equation in slope-intercept form, if possible.

Answer 1

The slope-intercept form of a line with slope m and y-intercept b is given by the following equation:

`y\text{ = mx+b}`

now, if the line that contains the point (-1,-2) is parallel to the line 5x+7y=12, then it has the same slope as this line, that is, the wanted line has the same slope as the line with equation 5x+7y=12. To find this slope, we must transform the equation 5x+7y=12 in the slope-intercept form:

`7y\text{ = -5x +12}`

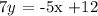
solving for y, this is equivalent to:

`y\text{ = -}(5)/(7)\text{x +}(12)/(7)`

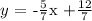
thus, the wanted line has the following slope:

`m\text{ = -}(5)/(7)`

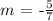
then, the provisional equation for this line is:

`y\text{ = -}(5)/(7)x+b`

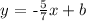
We only have to find the y-intercept. To achieve this, we must replace in the previous equation the coordinates of a point that belongs to the line and then solve for b. In this case, we can take the point (x,y)= (-1,-2), and we obtain:

`-2\text{ = -}(5)/(7)(-1)+b`

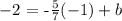
this is equivalent to:

`-2\text{ = }(5)/(7)+b`

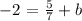
solving for b, we get:

`b\text{ = -2-}(5)/(7)\text{ =-}(19)/(7)`

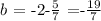
so that, we can conclude that the correct answer is:

`y\text{ = -}(5)/(7)x-(19)/(7)`