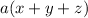Given:
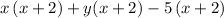
Required:
We need to factorize the given expressions.
Step-by-step explanation:
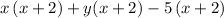
The common multiple in all terms is (x+2).
Take out the common term (x+2).
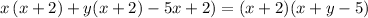
Final answer:
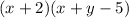
K)
Given:
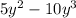
Step-by-step explanation:
The given expression can be written as follows.
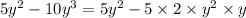
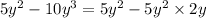
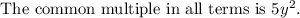
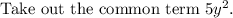
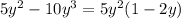
Final answer:
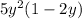
l)
Given:
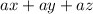
Step-by-step explanation:
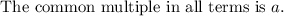
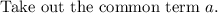
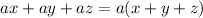
Final answer: