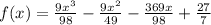Question

I wanted to see if I did it right since I’m studying for my test soon!

Answer 1

When a and b are the zeros of a function, this implies that

`\begin{gathered} x=a \\ \Rightarrow(x-a) \\ x=b \\ \Rightarrow(x-b) \end{gathered}`
`A(x-a)(x-b)=0`

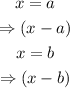
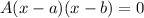
This implies the values of x when the function equals zero.

Given that the zeros of the cubic function f(x) are -6, 1 and 7, this implies that

`f(x)=A(x+6)(x-1)(x-7)\text{ ---- equation 1}`

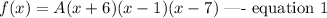
Given that

`f(8)=9`

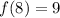
we substitute 9 for f(x) and 8 for x.

Thus,

`\begin{gathered} 9=A(8+6)(8-1)(8-7) \\ 9=A*14*7*1 \\ 9=98A \\ \Rightarrow A=(9)/(98) \end{gathered}`

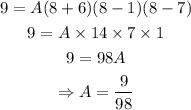
Substitute the value of A into equation 1.

`f(x)=(9)/(98)(x+6)(x-1)(x-7)`

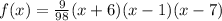
Expand the resulting equation.

`\begin{gathered} f(x)=(9)/(98)\mleft(x^2+5x-6\mright)\mleft(x-7\mright) \\ (9)/(98)(x-7)=\mleft((9x)/(98)-(9)/(14)\mright) \\ t\text{hus, we have} \\ f(x)=((9x)/(98)-(9)/(14))(x^2+5x-6) \\ =((9x)/(98)* x^2)+((9x)/(98)*\: 5x)+(9x)/(98)\mleft(-6\mright)-(9)/(14)x^2-((9)/(14)*\: 5x)-(9)/(14)\mleft(-6\mright) \\ \therefore f(x)=(9x^3)/(98)-(9x^2)/(49)-(369x)/(98)+(27)/(7) \end{gathered}`

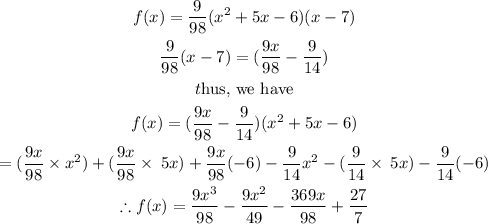
Hence, the equation for f(x) is

`f(x)=(9x^3)/(98)-(9x^2)/(49)-(369x)/(98)+(27)/(7)`