Question

Two closely spaced circular disks form a parallel-plate capacitor. Transferring 1,675,802,144.45 electrons from one disk to the other causes the electric field strength to be 926,331.13 N/C. What are the diameters, in mm, of the disks?

Answer 1

The electric field between the plates of a capacitor (assuming it is closely spaced) is given by:

`\vec{E}=(Q)/(\epsilon_0A)`

We can replace our values, and we'll get the following:

`926331.13=(1675802144.45*1.6*10^(-19))/(8.8541878*10^(-12)A)`

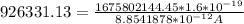
By isolating the are, we get:

`A=(1675802144.45*1.6*10^(-19))/(8.8541878*10^(-12)*926331.13)=3.269*10^(-5)m^2`

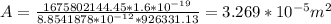
Now, if we replace it on the area of a circle:

`3.269*10^(-5)=\pi r^2`

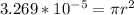
Our value of r is:

`r=\sqrt[\placeholder{⬚}]{(3.269*10^(-5))/(\pi)}=3.2258mm`

Then, our final answer is d=6.4515mm