SOLUTION:
We are to choose between a Cheez-it's that cover a rectangle with;
(i) A length of 9 and a perimeter of 22,
(ii) A length of 5 and a perimeter of 20.
The prefer one would be the one with a greater area.
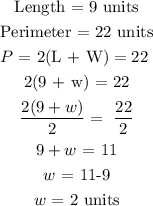
The area of this rectangle is;
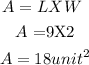
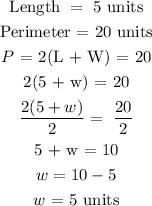
The area of this rectangle is;
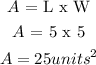
CONCLUSION:
Since the area of a rectangle of length of 5 and a perimeter of 20 is greater than that of a length of 9 and a perimeter of 22.
The preferred is the Cheez-it's that covers a rectangle of a length of 5 and a perimeter of 22.