Question

the first choice is- (is not) or (is)the second choice is- (are) or (are not)im thinking its- (is) and (are not)please correct me if im wrong

Answer 1

The identity matrix is the following.

`\begin{bmatrix}{1} & {0} & {} \\ {0} & {1} & {} \\ {} & {} & {}\end{bmatrix}`

We need to compute the product to find out whether it gives an identity matrix.

`\begin{bmatrix}{1} & {-3} & {} \\ {4} & {2} & {} \\ {} & {} & {}\end{bmatrix}\begin{bmatrix}{(1)/(5)} & {(3)/(10)} & {} \\ {-(2)/(5)} & {(1)/(10)} & {} \\ {} & {} & {}\end{bmatrix}=\begin{bmatrix}{(7)/(5)} & {0} & {} \\ {0} & {(7)/(5)} & {} \\ {} & {} & {}\end{bmatrix}`

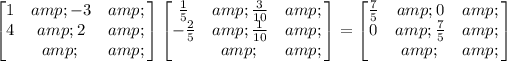
The result is not an identity matrix; therefore, the product of matrices is not an idenity matrix. Therefore, X and A are not inverse of each other.