1 Answer

Zizoo · Answer 1 · 2023-04-21T22:14:35+0000

Given:

Required:

To find the total surface area of the prism.

Step-by-step explanation:

The total surface area of the prism is given by the formula:

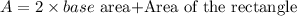
$A=2* base\text{ area+Area of the rectangle}$

Area of the base triangle

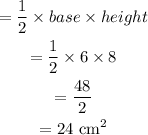
$\begin{gathered} =(1)/(2)* base* height \\ =(1)/(2)*6*8 \\ =(48)/(2) \\ =24\text{ cm}^2 \end{gathered}$

To find the width of the rectangle we will use the Pythagoras theorem.

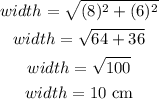
$\begin{gathered} width=√((8)^2+(6)^2) \\ width=√(64+36) \\ width=√(100) \\ width=10\text{ cm} \end{gathered}$

Area of the rectangle

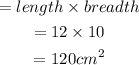
$\begin{gathered} =length* breadth \\ =12*10 \\ =120cm^2 \end{gathered}$

Thus the area of the prism

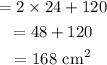
$\begin{gathered} =2*24+120 \\ =48+120 \\ =168\text{ cm}^2 \end{gathered}$

Final Answer:

Please log in or register to add a comment.