1 Answer

Andrepcg · Answer 1 · 2023-12-09T17:33:54+0000

Given the expression:

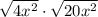
$√(4x^2)\cdot√(20x^2)$

You can simplify each Radical as follows, in order to find an equivalent expression:

1. If you decompose the coefficient 4 and the coefficient 20 into their Prime Factors, you get:

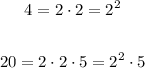
$\begin{gathered} 4=2\cdot2=2^2 \\ \\ 20=2\cdot2\cdot5=2^2\cdot5 \end{gathered}$

Rewrite the Radicands:

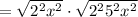
$=√(2^2x^2)\cdot√(2^25^2x^2)$

2. Apply this Property for Radicals:

$\sqrt[n]{b^n}=b$

Then, you get:

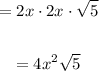
$\begin{gathered} =2x\cdot2x\cdot√(5) \\ \\ =4x^2√(5) \end{gathered}$

Hence, the answer is: Option A.

Please log in or register to add a comment.