The standard equation of a circle can be wriiten as;
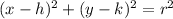
So, to get the value of h,k and r we need to express the given equation in this form.
The equation is given as;
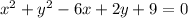
Then we will try to express this equation in the standard equation of circle form.
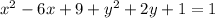
Note that we added 1 to both sides so that we can factorise the equation.
Factorizing, we have;
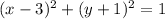
Then finally we have;
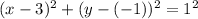
Comparing the equation to the standard form we have;
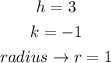
Then lastly we need to graph the equation;
From the graph, we can see that the only intercept we have is at;
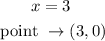
There is no intercept on the y axis.