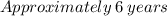
1) Since the initial population of rabbits consists of 200 animals and there is a constant growth of 30% so we can start out writing the exponential model for this problem, like this.
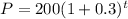
2) Let's plug P=1000 for the final population and solve for t:
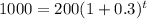
So, let's count 2015 as our first year since we don't know when there will be 1,000 rabbits.

Note the property of the exponents of logarithms