Question

Vertex: Axis of symmetry: x-intercept: Maximum or minimum: Max/Min value : y-intercept:

Answer 1

Vertex: (3/2, -3)

Axis of symmetry: x = 3/2

x-intercept: 0 and 3

Maximum or minimum: Minimum

Max/Min value: -3

y-intercept: 0

Step-by-step explanation

We have the quadratic function given in the question.

The vertex of a quadratic function (parabola) is the point where the parabola is either at its minimum or its maximum.

The parabola given has a minimum.

A quadratic function is generally given as:

`f(x)=ax^2\text{ + bx + c}`

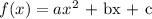
where a, b and c are coefficients

The x coordinate of the vertex is gotten by using:

x = - b / 2a

and the y coordinate is gotten by putting the x value in the function.

So, we have:

`\begin{gathered} x\text{ = -}(-4)/(2((4)/(3)))\text{ = -}(-4)/((8)/(3))\text{ = -(-4 }\cdot\text{ }(3)/(8)) \\ x=\text{ }(3)/(2) \end{gathered}`

This implies that:

`\begin{gathered} g(x)\text{ = }(4)/(3)((3)/(2))^2-\text{ 4(}(3)/(2)) \\ g(x)\text{ = 3 - 6} \\ g(x)\text{ = -3} \end{gathered}`

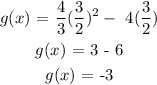
The vertex is (3/2, -3)

The axis of symmetry is given as the x coordinate of the vertex. That is:

x = 3/2

The x intercepts are the points where the function crosses the x axis (horizontal axis).

The x intercepts are 0 and 3.

The function has been determined to have a minimum value. The minimum value is the lowest value of the function. It is the y coordinate of the vertex.

Therefore, the minimum value is -3.

The y intercept is the point where the function crosses the y axis (vertical axis).

The y intercept is 0.