Question

Please answer which way is correct -1,-1/5 or the other way around

Answer 1

Hello there. To solve this question, we have to remember some properties about quadratic equations.

Given the following "quadratic" equation, we want to determine its solutions (if they exist) and the set of said solutions:

`x^(-2)+6x^(-1)+5=0`

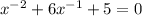
It is not exactly a quadratic equation, but doing the following substitution:

`y=(1)/(x)`

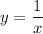
(as long the solutions to this equation are not zero, we're good), we'll get

`\begin{gathered} \left((1)/(y)\right)^(-2)+6\cdot\left((1)/(y)\right)^(-1)+5=0 \\ \\ y^2+6y+5=0 \\ \end{gathered}`

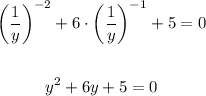
Solving it using the sum-to-product formula, we're looking for two roots such that

Their sum is equal to -6 and their product is equal to 5

In this case, both numbers have to be negative and satisfy these properties.

It is easy to see that the numbers will be:

`y=-5\text{ and }y=-1`

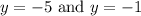
Now, we undo the substitution and solve for x:

`\begin{gathered} (1)/(x)=-5\Rightarrow x=-(1)/(5) \\ \\ (1)/(x)=-1\Rightarrow\,x=-1 \end{gathered}`

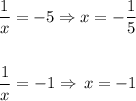
Therefore the set of solutions for this equation is:

`\left\{-(1)/(5),\,-1\right\}`

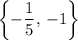
The order does not matter in this situation because the set

`\left\{-1\,-(1)/(5)\right\}`

Is the same as the other one, because it contains the same elements.