ANSWER
0.3783
Step-by-step explanation
The lengths of the pregnancies, X, is normally distributed with a mean of 246 days and a standard deviation of 13 days,
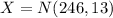
We have to find the probability that a randomly selected pregnancy lasts less than 242 days,
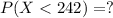
For this, we have to standardize the variable X with the formula,
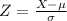
So the probability we have to solve is,
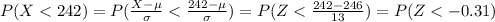
This is equivalent to,
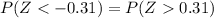
Which is also equivalent to,
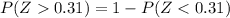
We have to find these equivalences because, usually, normal distribution tables show the probabilities for positive z-scores and to the left of those values - i.e. less than those values. Find z = 0.31 in a z-table,
So, the probability is,
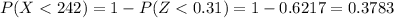
Hence, the probability that a randomly selected pregnancy lasts less than 242 days is 0.3783.