Alice has 36 possibilities of choosing ,Bob 126 and Kevin 84.
Alice, Bob and Kevin
7 different Flavors:
Chocolate
Vanillla
mint chip
strawberry
cookie dough
banana
caramel
The order of the 9 scoops does not matter.
_ _ _ _
a) How many ways can she choose her 9 scoops so she gets at least 1 scoop of each flavor?
Since there are 7 flavors, and she wants at least one of each then we have:
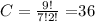
Alice has 36 possibilites of choosing
b) Bob
Since Bob can't eat too much he can't do no more than 4
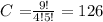
Bob has 126 possibilities of making his choice.
c) Kevin
3 scoups of banana or 3 scoups of strawberries.
Considering He wants 9 scoups.
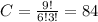
Kevin has 84 possibilities for banana or strawberries