Question

Find the equivalent resistance between points A and B shown in the figure(Figure 1). Consider R1 = 3.3 Ω , R2 = 4.5 Ω , R3 = 2.3 Ω , R4 = 3.7 Ω , R5 = 8.7 Ω , and R6 = 7.0 Ω .

Answer 1

the answer is 1.5 Ω

Step-by-step explanation

the rule to add resistance in parallel is:

`(1)/(R_(eq))=(1)/(R_1)+(1)/(R_2)+++(1)/(R_n)`

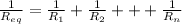
and, the rule to add resistances in serie is

`R_(eq)=R_1+R_2+R_3+...R_n`

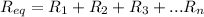
The total resistance of a series circuit is equal to the sum of individual resistances

so

Step 1

add the resistance in parallel :

so.Consider R1 = 3.3 Ω , R2 = 4.5 Ω , R3 = 2.3 Ω , R4 = 3.7 Ω , R5 = 8.7 Ω , and R6 = 7.0 Ω .

hence

left side:

`\begin{gathered} (1)/(R_(eq12))=(1)/(R_1)+(1)/(R_2) \\ (1)/(R_(eq12))=(1)/(3.3)+(1)/(4.5) \\ (1)/(R_(eq12))=0.5252 \\ R_(eq12)=(1)/(0.5252) \\ R_(eq12)=1.90 \end{gathered}`

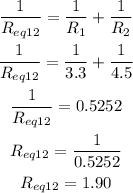
top

`\begin{gathered} (1)/(R_(eq345))=(1)/(R_3)+(1)/(R_(42))+(1)/(R_5) \\ hence \\ (1)/(R_(eq345))=(1)/(2.3)+(1)/(3.7)+(1)/(8.7) \\ (1)/(R_(eq345))=0.81999 \\ R_(eq345)=(1)/(0.8199) \\ R_(eq345)=1.2195 \end{gathered}`

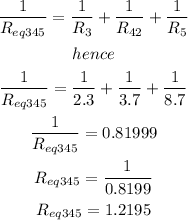
hence, we have the equivalent circuit

Step 2

b)now, w have resistance (345) and resistance 6 in serie, so we can add using the formula

`\begin{gathered} R_(eq)=R_1+R_2+R_3+...R_n \\ R_(345)a\text{ and R}_5\text{ are in serie , so} \\ R_(3456)=1.2195+7.0 \\ R_(3456)=8.2195 \end{gathered}`

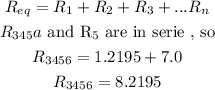
so, the new circuit would be

Step 3

finally, we have two resistances in parallel, so

.

`\begin{gathered} (1)/(R_(eq))=(1)/(R_(12))+(1)/(R_(3456)) \\ (1)/(R_(eq))=(1)/(1.90)+(1)/(8.2195) \\ (1)/(R_(eq))=0.6479 \\ isolate\text{ R}_(eq) \\ 1=0.6479\text{ *R}_(eq) \\ divide\text{ both sides by 0.6479} \\ (1)/(0.6479)=(0.6479*R_eq)/(0.6479) \\ hence \\ R_(eq)=1.543 \\ rounded \\ R_(eq)=1.5 \end{gathered}`

therefore, the answer is 1.5 Ω

I hope this helps you