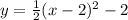Step 1
A)The given function is congruent to;
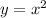
with the graph
For the vertex to open downwards. it means the required function will be a reflection of y=x².
There in the transformation to get the first step will be;
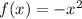
If the vertex is on the left of the y-axis then we will have the vertex form to be;

The vertex form of the part A will be;
![\begin{gathered} If\text{ we shift the required function 2 units to the left and 2 units up, the vertex becomes;} \\ (h,k)=(-2,2) \\ The\text{ Function opens downward which means its reflected. Hence, we will have;} \\ y=-1(x-(-2))^2+2 \\ y=-1(x+2)^2+2 \end{gathered}]()
Answer to the part A
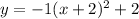
Step 2
If the function opens upwards, wider than y=x², with vertex below the x-axis and to the right of the y-axis, the function will be;
![\begin{gathered} upwards\text{ means no reflection and to the right of the y-axis means the vertex becomes} \\ (h,k)=(2,-2) \\ If\text{ it opens wider, it is a horizontal stretch and then a=<1} \\ Hence,\text{ the equation for part B could be} \\ y=(1)/(2)(x-2)^2-2 \end{gathered}]()
Answer to the part B;