1 Answer

Philask · Answer 1 · 2023-09-12T07:39:35+0000

We are asked to determine a polynomial that has the following roots:

$1+\sqrt[]{2},2-i$

As roots. We will use a polynomial of degree 4 that has the roots:

$1\pm\sqrt[]{2},2\pm i$

This means that the factors of the polynomials are:

$(x-(1+\sqrt[]{2})(x-(1-\sqrt[]{2}))(x-(2-i))(x-(2+i))$

Now we must expand the given factor in order to get a polynomial of rational coefficients. First, we will take the two first products:

$(x-(1+\sqrt[]{2})(x-(1-\sqrt[]{2}))$

Now we will reassociate terms inside each parenthesis:

$((x-1)-\sqrt[]{2})((x-1)+\sqrt[]{2}))$

Now we apply the distributive law using the associated terms:

$(x-1)^2+\sqrt[]{2}(x-1)-\sqrt[]{2}(x-1)-(\sqrt[]{2})^2$

Simplifying:

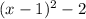
Therefore, the first two products can be replaced by the term we just found:

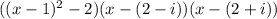
Now we take the third and fourth products:

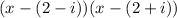
Now we reassociate the terms:

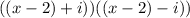
Now we apply the distributive law:

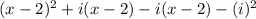
Simplifying we get:

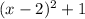
Now we can replace this for the third and fourth products:

Now we solve the squares in each parenthesis:

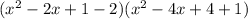
Adding like terms:

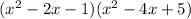
Now we apply the distributive property:

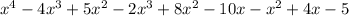
Adding like terms we get:

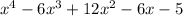
And thus we get the desired polynomial.

Please log in or register to add a comment.