Question

A family is booking a trip to Florida and the travel agent knows that for families with children of similar ages the probability of visiting Busch Gardens is 40% and the probability of visiting Sea World given that they visited Busch Gardens is 60%; also the agent knows the probability of this type of family visiting either Busch Gardens or Sea World is 70%. To determine the best package for this family, the agent wants to determine the probability that this family will visit Sea World without consideration to the fact that they visited Busch Gardens.

Answer 1

0.54 = 54% probability that this family will visit Sea World without consideration to the fact that they visited Busch Gardens.

Explanation:

We solve this question treating these events as Venn probabilities.

I am going to say that:

Event A: Visited Busch Gardens.

Event B: Visited Sea World.

The probability of visiting Busch Gardens is 40%

This means that
`P(A) = 0.4`

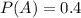
The probability of visiting Sea World given that they visited Busch Gardens is 60%

60% of 40%, which means that:

`P(A \cap B) = 0.6*0.4 = 0.24`

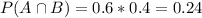
The agent knows the probability of this type of family visiting either Busch Gardens or Sea World is 70%.

This means that
`P(A \cup B) = 0.7`

Te agent wants to determine the probability that this family will visit Sea World without consideration to the fact that they visited Busch Gardens.

This is P(B).

These probabilities are related by the following equation:

`P(A \cup B) = P(A) + P(B) - P(A \cap B)`

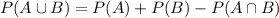
Replacing the values

`0.7 = 0.4 + P(B) - 0.24`

`0.16 + P(B) = 0.7`

`P(B) = 0.54`

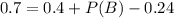
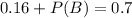
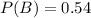
0.54 = 54% probability that this family will visit Sea World without consideration to the fact that they visited Busch Gardens.