Question

I am a little confused? What does the question want ?

Answer 1

The vertex of (f o g)(x) is on the x-axis while the vertex of (g o f)(x) is on the y-axis

Step-by-step explanation

First, we have to find the composite functions. In this notation, this means that we have to substitute x in the first function with the second function,

`(f\circ g)(x)=f(g(x))=(g(x))^2=(3x-2)^2`

Let's expand this function using the binomial squared rule,

`(3x-2)^2=(3x)^2-2\cdot3x\cdot2+2^2=9x^2-12x+4`

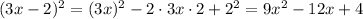
For the second composition, we have,

`(g\circ f)(x)=g(f(x))=3f(x)-2=3x^2-2`

Both composite functions are written in standard form,

`y=ax^2+bx+c`

The x-coordinate of the vertex is given by,

`x_v=(-b)/(2a)`

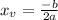
For the first composite function, a = 9, and b = -12,

`x_v=(-(-12))/(2\cdot9)=(12)/(18)=(2)/(3)`

And the y-coordinate of the vertex is,

`y_v=9x_v^2-12x_v+4=9\left((2)/(3)\right)^2-12\left((2)/(3)\right)+4=0`

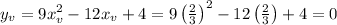
So, the vertex of the first composite function is at the point (2/3, 0).

For the second composite function, a = 3, and b = 0. This means that the x-coordinate of the vertex is 0 and the y-coordinate is,

`y_v=3\cdot0-2=-2`

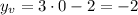
So, the vertex of the second composite function is at the point (0, -2).

Therefore, the vertices are located on each axis: the vertex of (f o g)(x) is on the x-axis while the vertex of (g o f)(x) is on the y-axis.