Given that
The function of revenue is R(x) = 100x - 0.2x^2
Explanation -
It is given that we have to find the number of rooms filled that gives maximum revenue.
And x is the number of rooms filled and R is the total revenue.
If the [Total revenue] value of the function is maximum it means its derivative is zero so we will find the derivative first.
Derivative of given function
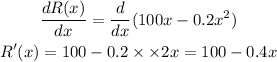
Since derivative of R(x) is zero then,
100 - 0.4x = 0
0.4x = 100
x = 100/0.4 = 1000/4 = 250
So the number of rooms filled to give maximum revenue is 250.
The final answer is 250.