Question

The functions y=log(x) is translated 1 united right and 2 units down. Which is the graph of the translated function.

Answer 1

In general, we can translate a function c units to the right by changing its argument this way:

`f(x)\to f(x-c)`

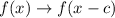
So, if we translate log(x) one unit to the right, we will get:

`\log (x-1)`

Now, in general, when we translate a function f(x) c units downwards, we obtain a new function, this is:

`f(x)\to f(x)-c`

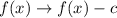
Then, in our case, we have already translated the function one unit to the right, after applying the translation downwards, we get:

`g(x)=\log (x-1)-2`

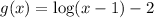
This is the function once we have transformed it

Finally, we need the graph that matches this equation, for this look at the value of x=2

`\begin{gathered} x=2 \\ \Rightarrow g(2)=\log (1)-2=-2 \\ \Rightarrow(2,-2) \end{gathered}`

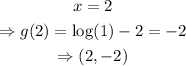
The graph must contain the point (2,-2). Thus, only the graph on the right top corner can be the graph of the function. The graph on the right top corner is the answer