We are given that a mass is attached to a string and is spun is in a horizontal circle, this means that the free body diagram of the problem is the following:
We will add the forces in the vertical direction:
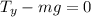
The forces add up to zero since there is no acceleration in the vertical direction. Therefore, we can add "mg" to both sides:
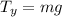
Now, The vertical component of the tension can be put in terms of the total tension using the following right triangle:
Therefore, we use the trigonometric function sine:
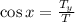
Multiplying both sides by "T"

Substituting in the sum of vertical forces:
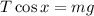
Now, Since the horizontal component of the tension is equivalent to the centripetal force, we have that:

Where:
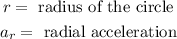
We can use the trigonometric function cosine to determine the horizontal component of the tension:

Multiplying both sides by "T":

Substituting we get:
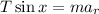
Now, we divide both equations:
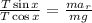
Simplifying we get;
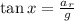
Now, we multiply both sides by "g":
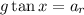
Now, in any circular motion, the period "P" is given by:

Where:
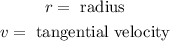
Also, the acceleration is given by:
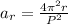
Substituting the expression for the acceleration we determined before we get:
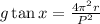
Substituting the expression for the period:

Solving the square:
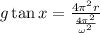
Solving the fraction:
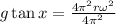
Simplifying:
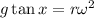
Now, we can put the radius in terms of the length of the spring using the following triangle:
using the function sine we get:

Substituting in the previous equation we get:
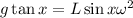
Now, we decompose the tangent:
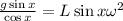
Simplifying:
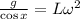
Now, we invert both sides:
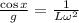
Multiplying both sides by "g" we get:
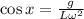
The angular velocity is the angle divided by time, since it takes 0.644 s to complete one revolution this means that :
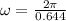
substituting the values:
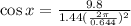
Solving the operations:
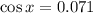
Now, going back to the sum of forces in the vertical direction:
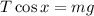
Dividing both sides by "g":
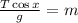
Substituting the values:
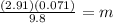
Solving the operations:
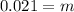
Therefore, the mass of the ball is 0.021 kg.