Question

the base and height of a parallelogram is (x-7)meters and (x+9)meters respectively.if the area of a paralellogram 192 square meters.find the actual values of its dimensions.

Answer 1

Given

The base and height of a parallelogram is (x-7)meters and (x+9)meters respectively.

`\begin{gathered} \text{Base(b) = (x-7)meters} \\ Height=\text{ (x+9)meters} \end{gathered}`

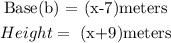
Formula

`\begin{gathered} \text{The area of a Paralelogram = Base}* Height \\ \end{gathered}`
`\text{The area is 192m}^2`

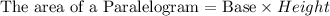
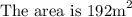
We now substitute into the formula

`\begin{gathered} 192=\mleft(x-7\mright)\mleft(x+9\mright) \\ 192=x^2+9x-7x-63 \\ 192=x^2+2x-63 \\ \text{REARRANGE} \\ x^2+2x-63-192=0 \\ x^2+2x-255=0 \\ \end{gathered}`

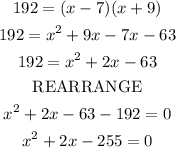
It is now Quadratic Equation

`\begin{gathered} a=1,\text{ b=2 and c=-255} \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ We\text{ can now substitute into the quadratic formula} \\ x=\frac{-2\pm\sqrt[]{2^2^{}-4*1*-255}}{2*1} \\ \\ x=\frac{-2\pm\sqrt[]{4^{}--1020}}{2} \\ \\ \end{gathered}`
`\begin{gathered} x=\frac{-2\pm\sqrt[]{1024}}{2} \\ \\ x=(-2\pm32)/(2) \\ \\ x=(-2+32)/(2)=(30)/(2)=15 \\ \\ or \\ x=(-2-32)/(2)=-(34)/(2)=-17 \end{gathered}`

For distance or dimension it can't be negative, so we choose the positive

x=15

Recall from the question

Base=(x-7)meters

Height= (x+9)meters

We can now replace x with 15

`\begin{gathered} \text{Base}=\text{ 15-7} \\ \text{Base}=8m \\ \\ \text{Height =15+9} \\ \text{Height}=24m \end{gathered}`

The final answer

Base is 8m

Height is 24m