Question

Find the area of the shaded sector it the radius of the circle is 1.5

Answer 1

We are given a circle with a radius equal to 15

We know that a full-circle corresponds to 360°.

Whereas a semi-circle corresponds to 180°.

So, the angle corresponding to the shaded region can be found as

`180\degree-45\degree=135\degree`

Now we can use the following formula to find the area of the shaded sector.

`A=(\theta*\pi)/(360\degree)* r^2`

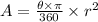
Where r is the radius of the circle and θ is the angle of the shaded sector (that is 135°)

Let us substitute the given values into the above formula to get the area of the shaded sector.

`\begin{gathered} A=(135\degree*\pi)/(360\degree)*15^2 \\ A=(3\pi)/(8)*225 \\ A=(675\pi)/(8) \\ A=265.07 \end{gathered}`

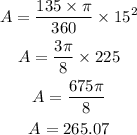
Therefore, the area of the shaded sector is 265