Question

The lengths of pregnancies in a small rural village are normally distributed with a mean of 261 days and a standard deviation of 12 days.a. In what range would you expect to find the middle 50% of most pregnancies?Between and .b. If you were to draw samples of size 37 from this population, in what range would you expect to find the middle 50% of most averages for the lengths of pregnancies in the sample?Between and .

Answer 1

a. 269.1 and 252.9

b. 262.3 and 259.6

Explanation:

Given:

mean = 261days

standard deviation = 12days

We use the normal table to calculate the value of z, like this:

a.

Therefore, the middle 50% are from 269.1 and 252.9

b.

n = 37

`\begin{gathered} \sigma_{\bar{x}}=\frac{\sigma}{\sqrt[]{n}} \\ \sigma_{\bar{x}}=\frac{12}{\sqrt[]{37}} \\ \: \sigma_{\bar{x}}=1.97 \end{gathered}`

Using z-score formula:

`\begin{gathered} \bar{x}=\pm z\cdot\sigma_{\bar{x}}+\mu \\ \bar{x}=0.6745\cdot1.97+261=262.3 \\ \bar{x}=-0.6745\cdot1.97+261=259.6 \end{gathered}`

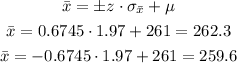
Therefore, the middle 50% are from 262.3 and 259.6