It describes an hyperbola (option D)
Step-by-step explanation:
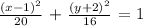
An ellipse is in the form:

A parabola is in the form:
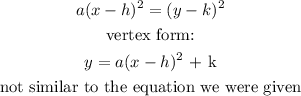
An equation of circle has a radius in the formula which is not in the given formula. Hence, it can't be circle.
An hyperbola is in the form:
![\begin{gathered} ((x-h)^2)/(a^2)\text{ - }((y-k)^2)/(b^2)\text{ = 1} \\ \text{where h = 1, k = -2, a = }\sqrt[]{20},\text{ b = }\sqrt[]{16} \\ \text{this is similar in form to the equation given} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tpue6ehiot1up4kgmx8wnn5upezhbp385p.png)