Question

A cylinder hydraulic press has a small piston with a diameter of 3 m, and the diameter of the large piston is unknown. Suppose a force of 800 N is applied onto the small piston to lift the 250 kg load. The hydraulic press follows Pascal principle.Calculate the diameter of the large piston and estimate the force needed if additional load of 50 kg is added.

Answer 1

In order to determine the diameter of the larger piston, use the following formula for the Pascal principle:

`(F_1)/(A_1)=(F_2)/(A_2)`

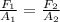
where F1 and F2 are the forces applied to pistons with area A1 (smaller piston) and A2 (larger piston).

Take into account that the force on the larger piston is the weight related to 250kg load. Then, the force is:

F2 = M*g = (250 kg)(9.8 m/s^2) = 2450N

Moreover, consider that the area of a circle shape is:

`A=\pi r^2`

where r is the radius. In this case, for the smaller piston, you have r1 = 3/2 m = 1.5 m. Then, the area is:

`A_1=(3.14)(1.5m)^2\approx7.1m^2`

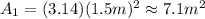
Then, use F1 = 800N and solve for A2 in the equation for Pascal principle:

`A_2=(F_2)/(F_1)\cdot A_1=(2450N)/(800N)\cdot7.1m^2=21.7m^2`

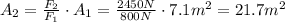
Finally, use the formula for the area of a circle to find the radius of the larger piston:

`\begin{gathered} A_2=\pi r^2_2 \\ r_2=\sqrt{(A_2)/(\pi)}=\sqrt[]{(21.7m^2)/(3.14)}=2.63m \end{gathered}`

Hence, the diameter of the large piston is

d = 2*r = 2(2.63m) = 5.26m

If additional load of 50kg is added, then, the required force becomes:

`F_2=(A_2)/(A_1)\cdot F_1=(21.7m^2)/(7.1m^2)\cdot(250kg+50kg)(9.8(m)/(s^2))=8985.6N`

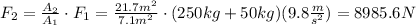
Hence, the needed force would be 8985.6N