we have the equation

Group similar terms and move the constant term to the right side
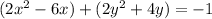
Factor the leading coefficient on both terms of the left side
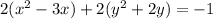
Complete the square twice
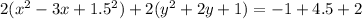
Rewrite as a perfect square
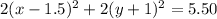
Divide both sides by 2
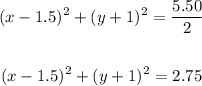
we have the equation of a circle
therefore
The answer is a circle