For this problem, we have a triangular prism and its measurements. We need to determine the volume for the solid.
The volume of a triangular prism can be found with the following equation:
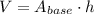
Where the area of the base, which is the triangular face, can be determined with:
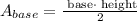
Applying the given information to both expressions, we have:
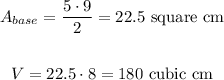
The volume of the triangular prism is equal to 180 cm³.