Question

Could you please help me see the steps on this question?

Answer 1

Given the absolute inequality

`2|x+3|+1>3`

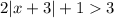
The absolute in equality can be written as:

`\begin{gathered} 2|x+3|+1>3 \\ 2|x+3|>3-1 \\ |x+3|>(2)/(2) \\ |x+3|>1 \end{gathered}`

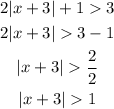
Sloving the inequality above, we can split it into two, then we will have;

`\begin{gathered} -1>|x+3|\text{and }|x+3|>1 \\ \end{gathered}`

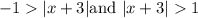
Solving the left hand side equation

`\begin{gathered} |x+3|<-1 \\ x<-3-1 \\ x<-4 \end{gathered}`

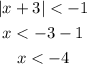
To solve for the right hand side we have

`\begin{gathered} |x+3|>1 \\ x+3>1 \\ x>1-3 \\ x>-2 \end{gathered}`

The graph of the inequality on the number line is shown below

Hence the solution of the inequality is x< -4 and x> -2