The table given shows the calculation of the variance and standard deviation of a given sample.
The formula for the variance is given as shown below;
![\begin{gathered} S^2=(\Sigma(x_i-\mu)^2)/(n-1) \\ \text{Where;} \\ S^2=S\tan dard\text{ deviation} \\ \Sigma=Summation(addition) \\ x_i=value\text{ from observed data} \\ \mu=\operatorname{mean}\text{ from the observed data} \\ n=\text{sample size} \end{gathered}]()
When we substitute for the values given, this becomes;
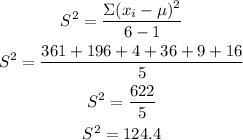
Therefore, the missing value is 622.
This is the addition of each observed data minus the mean (that is, the addition of the third column).