Question

Harrison has an account with the balance of $155.59 this account has an interest rate of 9.4 % compound annually and the initial investment was two years ago. How much was the initial investment?

Answer 1

To answer this problem, we need to use the compound interest formula, which is

`A=P(1+(r)/(n))^(nt)`

Where A represents the final amount, P represents the principal(initial investment), r represents the interest rate in decimals, n represents the number of times interest is compounded per unit t, and t the amount of time.

We have the final balance of Harrison's account, which is our value A

`A=155.59`

The interest rate is 9.4%. To convert a percentage to a decimal, we just divide the percentage value by 100.

`r=9.4\%=(9.4)/(100)=0.094`

The initial investment was two years ago, therefore, the time period is 2.

`t=2`

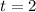
And since the interest is compounded anually and the time period unit is year, we have

`n=1`

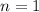
Plugging all those values in the formula, we have

`155.59=P(1+(0.094)/(1))^(1\cdot2)`

Solving for P, we have

`\begin{gathered} 155.59=P(1+(0.094)/(1))^(1*2) \\ 155.59=P(1.094)^2 \\ P=130.001102908... \\ P\approx130.00 \end{gathered}`

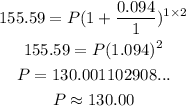
The initial investment was $130.00.